Cebirden Geometriye: Denklemler

Birçok kişi için matematik, semboller ve denklemlerle dolu karmaşık bir dil gibi görünebilir. Ancak bu sembollerin arkasında yatan anlamı keşfettiğinizde, matematiksel cebirden geometriye geçişin ne kadar akıcı olduğunu göreceksiniz. Bugünkü konumuz, ikinci dereceden fonksiyonların grafiğini oluşturan denklem ( f(x) = ax^2 + bx + c ) üzerine olacak.

1. Parabolün Temeli

İkinci dereceden bir fonksiyon olan ( f(x) = ax^2 + bx + c ), koordinat düzleminde bir parabol oluşturur. Bu fonksiyonun grafiğindeki her nokta, x’in alabileceği her değer için y’nin aldığı değerle eşleşir.

2. Katsayıların Rolü

• a Katsayısı: Bu katsayı, parabolün yönünü ve genişliğini belirler.
• a > 0 ise, parabol yukarı doğru açılır.
• a < 0 ise, parabol aşağı doğru açılır.
• |a|’nın büyüklüğü parabolün genişliğini etkiler; büyükse dar, küçükse geniş bir parabol oluşturur.
• b Katsayısı: b katsayısı, parabolün x eksenine göre olan konumunu ve eğimini etkiler.
• c Katsayısı: c, fonksiyonun y eksenini kestiği noktadır. Başka bir deyişle, x = 0 olduğunda y’nin aldığı değerdir.

3. Tepe/Tepenoktası

Parabolün tepe noktası, parabolün en yüksek ya da en düşük noktasıdır ve bu nokta ((-b/2a, f(-b/2a))) ile bulunur.

4. Kökler ve x-kesişimleri

Parabolün x eksenini kestiği noktalara kök ya da sıfır denir. Bu noktaları bulmak için ( ax^2 + bx + c = 0 ) denkleminin köklerini bulmamız gerekir. Eğer gerçek kökler bulunamazsa, parabol x eksenini kesmez.

5. Görselleştirme

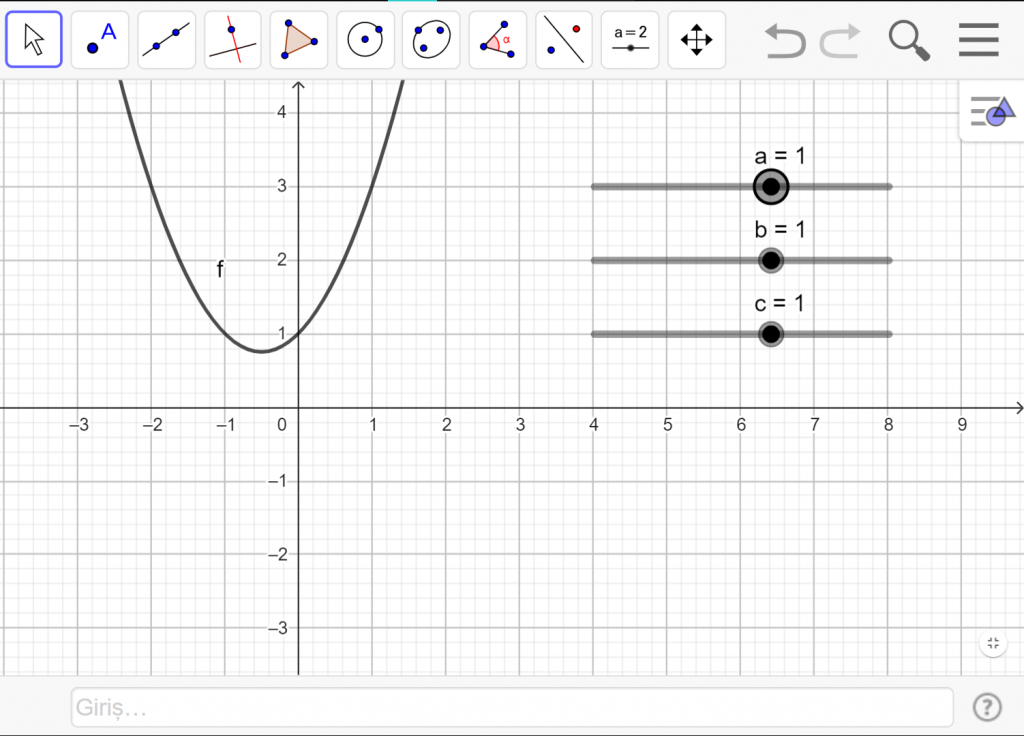
Modern teknoloji sayesinde, bu tür denklemlerin grafiğini kolayca çizebiliriz. Programlar ve uygulamalar (örneğin GeoGebra), bu denklemlerin grafiğini anında oluşturabilir. Özellikle değişken katsayılarla denklemlerin nasıl değiştiğini görselleştirmek için bu araçlar son derece kullanışlıdır.

Sonuç

Denklemler, matematiğin soyut bir dilidir, ancak bu denklemleri görselleştirdiğinizde, bu soyut kavramların aslında somut, elle tutulur gerçekliklere nasıl dönüştüğünü görebilirsiniz. ( f(x) = ax^2 + bx + c ) gibi basit bir denklemin bile, birçok farklı hikayeyi nasıl anlattığını keşfetmek, matematiğin güzelliklerinden biridir.

Unutmayın, matematiksel denklemler sadece rakamlar ve sembollerden ibaret değildir; onlar, doğanın ve evrenin dilini konuşan birer hikayecidir. Bu dilde ne kadar yetenekli olursanız, etrafınızdaki dünyayı o kadar derinlemesine anlarsınız.

Etkinliğe erişmek için tıklayınız.